Packages and LLMs
Modern Plain Text Social Science
Week 13
Duke University
December 2025
Bonus Helpers
Code Formatters
- Air is a fast code-formatter for R code.
- It integrates with RStudio and Positron; you can also use it from the command line.
- The idea is that it automatically formats your code according to tidyverse (or some other) style gude, every time you save your file. Or you can select some code and tell it to format that.
- Right now it works on
Rscript files but notqmdfiles.
Linters
- A linter is a tool that does “static analysis” of your code and then points out (and potentially corrects) errors and issues. It’s like one step beyond a code formatter.
- Jarl is a new linter for R code that is much faster than its main alternative,
lintr. It’s built on top of Air. - Again, you can use it from the command line to check specific fiels or integrate it with RStudio or Positron so that it lives in your IDE and keeps an eye on what you’re doing.
- Linters check against rules of various kinds that you can choose to enforce or not.
Packages
Projects
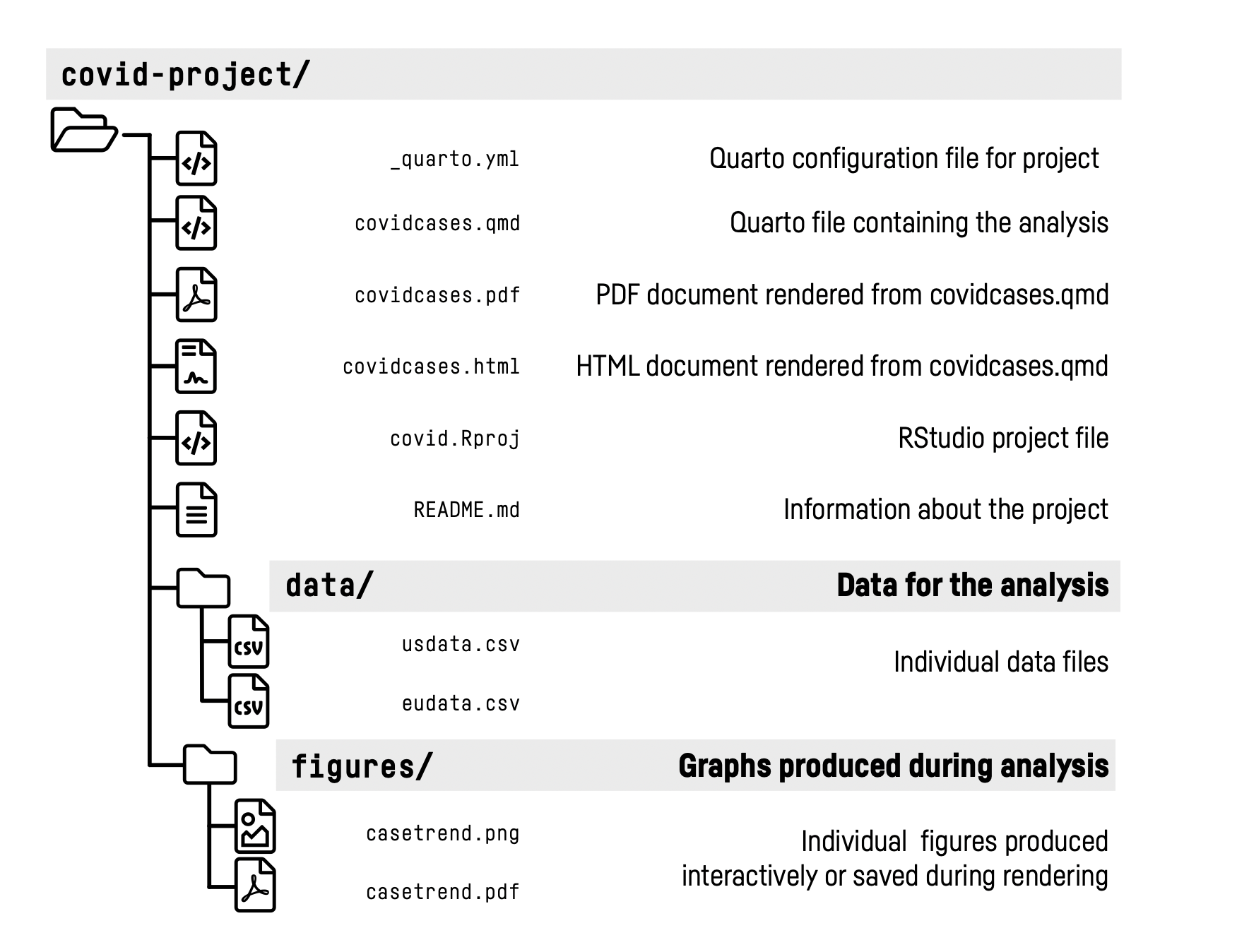
Packages
You already know that …
- R packages can be installed from CRAN, GitHub, or other sources, and they can be loaded into R using the
library()function. - R packages are collections of functions, data, and documentation.
- Every R package we’ve used has documentation that you can access with
?packagename - Many packages we’ve used have a website associated with them.
- It’s very handy to have a system for bundling up code or data in a way that makes it immediately available in your R environment and that can be guaranteed to work on anywhere it can be installed.
Package Structure
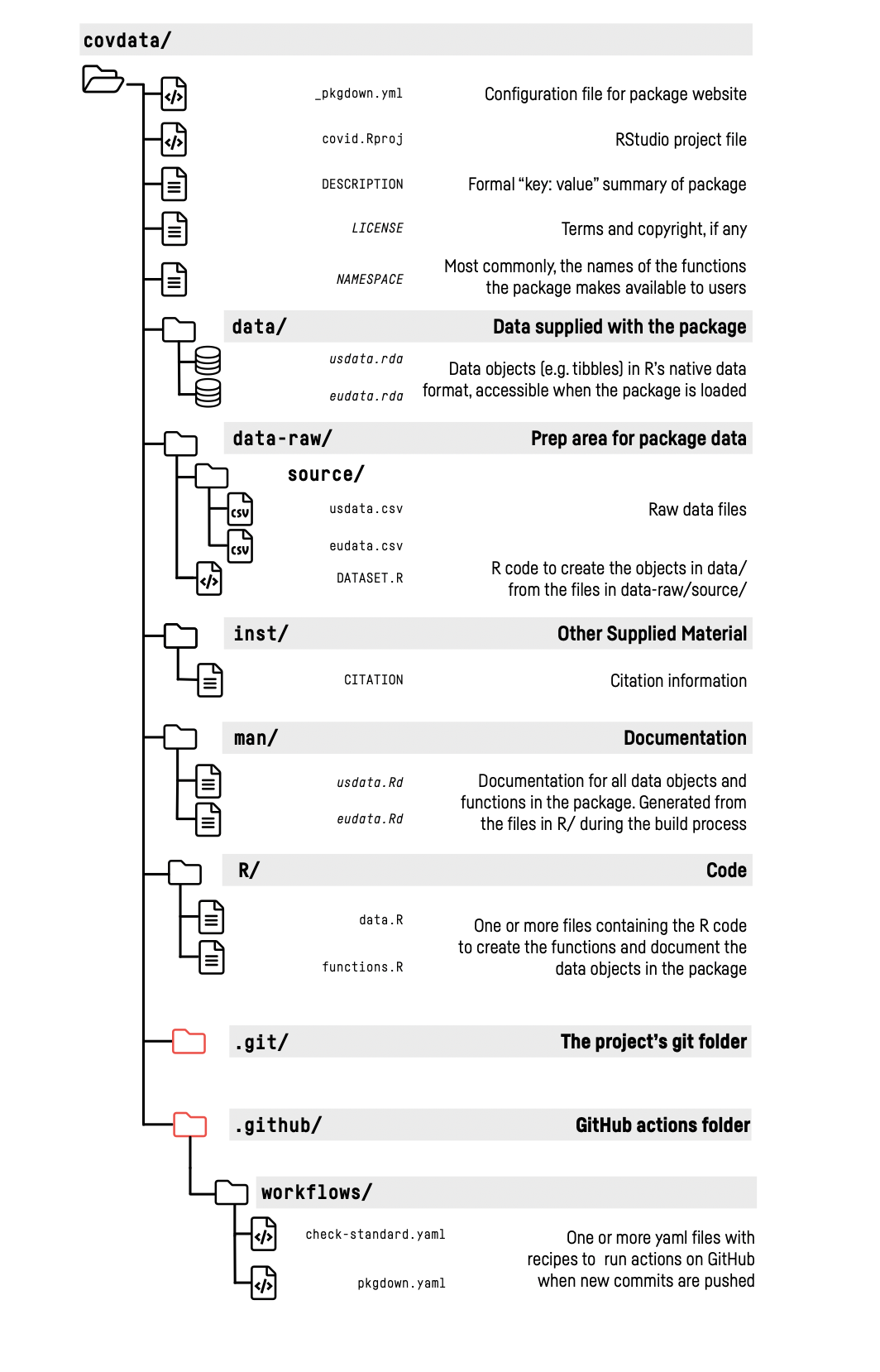
- A package is a special project with a prescribed structure.
- Packages hold you to a higher standard than projects. You should expect them to pass a battery of checks and tests via the
devtools::check()function. - With a package you can also hook into automated testing, continuous integration, and other tools that help ensure your code works as intended.
usethis package workflow
create_package()use_git(),use_github()(as you would in a project)use_data_raw(),use_data()use_mit_license()(or other license)use_readme_rmd()- Many more specialized functions available too for tests, vignettes, etc.
pkgdown workflow
The pkgdown package makes it easy to build a website for your package.
usethis::use_pkgdown()usethis::use_pkgdown_github_pages()pkgdown::build_site()
LLMs
Large Language Models
- You should have a clear mental model of what LLMs are and how they work.
- Things continue to move fast in this area.
- There are a lot of ways to incorporate them (or not) into your work.
- Pick your analogy: Minion Army, Forklift at the Gym, Plagiarism Machine.
You are responsible.
General Use Categories
- As a chatbot helping you, in effect, search the documentation.
- As a chatbot helping you write small pieces of code.
- As an Agent, integrated into your IDE, allowed to edit files and run tools.
- As an API you can call from R to do things that LLMs are distinctively good at.
Code-writing use cases
How should you think about the case where you’re using an LLM to help you write code?
- Here’s a very rough analogy: Find the Prime Factors of 91.
Code-writing use cases
Here’s a very rough analogy: Find the Prime Factors of 91.
You need to try dividing by primes: 2, 3, 5, 7, 11, 13…
91 ÷ 2? No (91 is odd)
91 ÷ 3? No (9+1=10, not divisible by 3)
91 ÷ 5? No (doesn’t end in 0 or 5)
91 ÷ 7? Yes. 91 = 7 × 13
This took several steps and required knowledge of primes up to √91 ≈ 9.5.
Code-writing use cases
Check the answer:
7 × 13 = 91 ✓
Maybe we have more clever ways of figuring out the division steps, starting from just keeping a list of all the numbers we know are prime. But the checking step is going to be faster and easier than the solving step.
Code-writing use cases
Now find the prime factors of
1522605027922533360535618378132637429718068114961380688657908494580122963258952897654000350692006139(This is RSA-100).
Code-writing use cases
Now find the prime factors of
1522605027922533360535618378132637429718068114961380688657908494580122963258952897654000350692006139They are:
37975227936943673922808872755445627854565536638199
× 40094690950920881030683735292761468389214899724061Finding the prime factors of a really large number is extremely hard. There is no efficient method for it. Checking whether two given large primes multiply to a given large number, on the other hand, is easy. (This is the basis of public-key cryptography.)
A very rough analogy
- “Hard to Solve but Easy to Check” is a very important category of problems.
- If you use LLMs to help you write code, you are in something very roughly like this position. You don’t know how to solve the problem or find the answer. But you can check whether any particular answer is correct or not.
- You still have to do the work of checking! And you still have to do the work of understanding what a correct answer looks like.
- If you cannot check the answer, or do not know how to check the answer, then you should not be using an LLM to help you write code.
General Use Categories
- As a Chatbot helping you write code.
- As an Agent, integrated into your IDE.
- As an API you can call from R.
Let’s work through some examples, live.